MaTeMaTiCaS - IDENTIDADES TRIGONOMETRICAS

En matemática, las identidades trigonométricas son igualdades que involucran funciones trigonométricas, verificables para cualquier valor permisible de la variable o variables que se consideren (es decir para cualquier valor que pudieran tomar los ángulos sobre los que se aplican las funciones).

Estas identidades son útiles siempre que se precise simplificar expresiones que incluyen funciones trigonométricas. Otra aplicación importante es el cálculo de integrales de funciones no-trigonométricas: se suele usar una regla de sustitución con una función trigonométrica, y se simplifica entonces la integral resultante usando identidades trigonométricas.

Notación: Definimos cos², sen², etc; tales que sen²α es (sen (α))².

Relaciones básicas [editar]

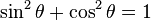Relación pitagórica	$sin^2 theta + cos^2 theta = 1,$
Identidad de la razón	$tan theta = frac{sin theta}{cos theta}$

De estas dos identidades, se puede extrapolar la siguiente tabla. Sin embargo, nótese que estas ecuaciones de conversión pueden devolver el signo incorrecto (+ or −). Por ejemplo, si sin θ = 1/2, la conversión propuesta en la tabla indica que 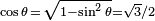$scriptstylecostheta,=,sqrt{1 - sin^2theta} = sqrt{3}/2$ , aunque en realidad $scriptstylecostheta ,=, -sqrt{3}/2$ . Para obtener la única respuesta correcta se necesitará saber en qué cuadrante está θ.

Funciones trigonométricas en función de las otra cinco.
Función	sin	cos	tan	csc	sec	cot
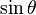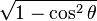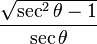$sinθ =$	$sin theta$	$sqrt{1 - cos^2theta}$	$frac{tantheta}{sqrt{1 + tan^2theta}}$	$frac{1}{csc theta}$	$frac{sqrt{sec^2 theta - 1}}{sec theta}$	$frac{1}{sqrt{1+cot^2theta}}$
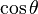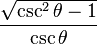$cosθ =$	$sqrt{1 - sin^2theta}$	$cos theta$	$frac{1}{sqrt{1 + tan^2 theta}}$	$frac{sqrt{csc^2theta - 1}}{csc theta}$	$frac{1}{sec theta}$	$frac{cot theta}{sqrt{1 + cot^2 theta}}$
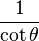$tanθ =$	$frac{sintheta}{sqrt{1 - sin^2theta}}$	$frac{sqrt{1 - cos^2theta}}{cos theta}$	$tan theta$	$frac{1}{sqrt{csc^2theta - 1}}$	$sqrt{sec^2theta - 1}$	$frac{1}{cot theta}$
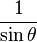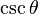$cscθ =$	${1 over sin theta}$	${1 over sqrt{1 - cos^2 theta}}$	${sqrt{1 + tan^2theta} over tan theta}$	$csc theta$	${sec theta over sqrt{sec^2theta - 1}}$	$sqrt{1 + cot^2 theta}$
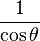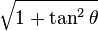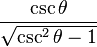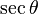$secθ =$	${1 over sqrt{1 - sin^2theta}}$	${1 over cos theta}$	$sqrt{1 + tan^2theta}$	${csctheta over sqrt{csc^2theta - 1}}$	$sectheta$	${sqrt{1 + cot^2theta} over cot theta}$
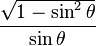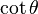$cotθ =$	${sqrt{1 - sin^2theta} over sin theta}$	${cos theta over sqrt{1 - cos^2theta}}$	${1 over tantheta}$	$sqrt{csc^2theta - 1}$	${1 over sqrt{sec^2theta - 1}}$	$cottheta$

De las definiciones de las funciones trigonométricas [editar]

$tan{x} = frac {sin{x}} {cos{x}} qquad cot{x} = frac{1} {tan{x}} = frac{cos{x}}{sin{x}}$

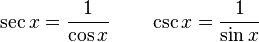
$sec{x} = frac{1} {cos{x}} qquad csc{x}= frac{1}{sin{x}}$

Son más difíciles de probar en la circunferencia trigonométrica o goniométrica (tiene radio=1):

$sin(x) = sin(x + 2pi) qquad cos(x) = cos(x + 2pi) qquad tan(x) = tan(x + pi)$

$sin(-x) = -sin(x) qquad cos(-x) = cos(x)$

$tan(-x) = -tan(x) qquad cot(-x) = -cot(x)$

$sin(x) = cosleft(frac{pi}{2} - xright) qquad cos(x) = sinleft(frac{pi}{2}-xright) qquad tan(x) = cotleft(frac{pi}{2} - xright)$

A veces es importante saber que cualquier combinación lineal de una serie de ondas senoidales que tienen el mismo período pero están desfasadas, es también una onda senoidal del mismo período pero con un desplazamiento de fase diferente. Dicho de otro modo:

$asin(x)+bcos(x)=sqrt{a^2+b^2}cdotsinleft( x+arctan{frac{b}{a}} right)$

$sin^2left(xright)+cos^2left(xright)=1$

Es llamada identidad trigonométrica fundamental, y efectuando sencillas operaciones permite encontrar unas 24 identidades más, muy útiles para problemas introductorios del tipo conocido el valor de la función seno, obtenga el valor de las restantes (sin tabla ni calculadora).

Por ejemplo, si se divide ambos miembros por cos², se tiene:

$tan^2left(xright)+1 = sec^2left(xright)$

Calculando la recíproca de la expresión anterior:

$cot^2left(xright) + 1 = csc^2left(xright)$

Entonces puede expresarse la función seno según alguna otra conocida:

$sin(x) = sqrt{1-cos^2(x)} qquad sin(x) = frac {1} {sqrt{1+tan^{-2}(x)}}$

$sin(x) = frac {1} {sqrt{1+cot^2(x)}} qquad sin(x) = frac{1} {sec{x}} sqrt{sec^2(x)-1}$

y análogamente con las restantes funciones .

Teoremas de la suma y diferencia de ángulos [editar]

Pueden demostrarse según la Fórmula de Euler o mediante la proyección de ángulos consecutivos. La identidad de la tangente surge del cociente entre coseno y seno, y las restantes de la recíproca correspondiente.

$sin(x pm y) = sin(x) cos(y) pm cos(x) sin(y)$

$cos(x pm y) = cos(x) cos(y) mp sin(x) sin(y)$

$tan(x pm y) = frac{tan(x) pm tan(y)}{1 mp tan(x)tan(y)}$

De lo que se sigue para determinados ángulos suplementarios:

$sin(pi pm x) = mpsin(x)$

$cos(pi pm x) = -cos(x)$

$tan(pi pm x) = pmtan(x)$

$csc(pi pm x) = mpcsc(x)$

Para ángulos complementarios:

$sinleft(frac{pi}{2} - xright) = cos(x)$

$cosleft(frac{pi}{2} - xright) = sin(x)$

$tanleft(frac{pi}{2} - xright) = cot(x)$

$cscleft(frac{pi}{2} - xright) = sec(x)$

$secleft(frac{pi}{2} - xright) = csc(x)$

$cotleft(frac{pi}{2} - xright) = tan(x)$

Para ángulos opuestos:

$sinleft(-xright) = -sinleft(xright)$

$cosleft(-xright) = cosleft(xright)$

$tanleft(-xright) = -tanleft(xright)$

$cscleft(-xright) = -cscleft(xright)$

$secleft(-xright) = secleft(xright)$

$cotleft(-xright) = -cotleft(xright)$

Identidades del ángulo múltiple [editar]

Si T_n es el n-simo Polinomio de Chebyshev entonces

$operatorname{cos}(nx)=T_n(cos(x)).$

Fórmula de De Moivre:

$operatorname{cos}(nx)+isin(nx)=(cos(x)+isin(x))^n$

Identidades del ángulo doble, triple y medio [editar]

Pueden obtenerse remplazándolo y por x (o sea $sin(x + x) = sin(2 x)$ ) en las identidades anteriores, y usando Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando $n = 2$ .

Fórmula del ángulo doble
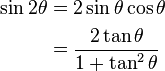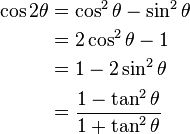$begin{align} sin 2theta &= 2 sin theta cos theta \ &= frac{2 tan theta} {1 + tan^2 theta} end{align}$	$begin{align} cos 2theta &= cos^2 theta - sin^2 theta \ &= 2 cos^2 theta - 1 \ &= 1 - 2 sin^2 theta \ &= frac{1 - tan^2 theta} {1 + tan^2 theta} end{align}$	$tan 2theta = frac{2 tan theta} {1 - tan^2 theta},$	$cot 2theta = frac{cot theta - tan theta}{2},$
Fórmula el ángulo triple
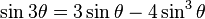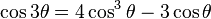$sin 3theta = 3 sin theta- 4 sin^3theta ,$	$cos 3theta = 4 cos^3theta - 3 cos theta ,$	$tan 3theta = frac{3 tantheta - tan^3theta}{1 - 3 tan^2theta}$
Fórmula del ángulo medio
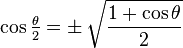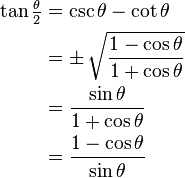$sin tfrac{theta}{2} = pm, sqrt{frac{1 - cos theta}{2}}$	$cos tfrac{theta}{2} = pm, sqrt{frac{1 + costheta}{2}}$	$begin{align} tan tfrac{theta}{2} &= csc theta - cot theta \ &= pm, sqrt{1 - cos theta over 1 + cos theta} \ &= frac{sin theta}{1 + cos theta} \ &= frac{1-cos theta}{sin theta} end{align}$	$cot tfrac{theta}{2} = csc theta + cot theta$

Producto infinito de Euler [editar]

$cosleft({theta over 2}right) cdot cosleft({theta over 4}right) cdot cosleft({theta over 8}right)cdots = prod_{n=1}^infty cosleft({theta over 2^n}right) = {sin(theta)over theta}.$

Identidades para la reducción de exponentes [editar]

Resuelve las identidades tercera y cuarta del ángulo doble para cos²(x) y sin²(x).

Seno	$sin^2theta = frac{1 - cos 2theta}{2}$	$sin^3theta = frac{3 sintheta - sin 3theta}{4}$
Coseno	$cos^2theta = frac{1 + cos 2theta}{2}$	$cos^3theta = frac{3 costheta + cos 3theta}{4}$	$cos^5theta = frac{10 costheta + 5 cos 3theta + cos 5theta}{16}$
Otros	$sin^2theta cos^2theta = frac{1 - cos 4theta}{8}$	$sin^3theta cos^3theta = frac{sin^3 2theta}{8}$

Identidades del medio ángulo [editar]

Reemplazando x/2 por x en las anteriores, es posible resolver cos(x/2) y sin(x/2).

$left|cosleft(frac{x}{2}right)right| = sqrt{left(frac{1 + cos(x)}{2}right)}$

$left|sinleft(frac{x}{2}right)right| = sqrt{left(frac{1 - cos(x)}{2}right)}$

Multiplicando tan(x/2) por 2cos(x/2) / ( 2cos(x/2)) y reemplazando sin(x/2) / cos(x/2) por tan(x/2). El numerador es entonces sin(x) por la identidad del ángulo doble, y el denominador es 2cos²(x/2) - 1 + 1 que es cos(x) + 1 por la identidad del ángulo doble. La segunda identidad se obtiene multiplicando la primera por sin(x) / sin(x) y simplificando mediante la identidad pitagórica.

$tanleft(frac{x}{2}right) = frac{sin(x)}{cos(x) + 1} = frac{1 - cos(x)}{sin(x)}$

Paso de Producto a Suma [editar]

Puede probarse usando el teorema de la suma para expandir los segundos miembros.

$cos(x) cos(y) = {cos(x + y) + cos(x - y) over 2}$

$sin(x) sin(y) = {cos(x - y) - cos(x + y) over 2}$

$cos(x) sin(y) = {sin(y + x) + sin(y - x) over 2}$

¿De donde se origina $cos(x) cos(y) = {cos(x + y) + cos(x - y) over 2}$ ? [editar]

Esta explicación muestra como obtener la formula anterior paso por paso (en otras palabras, es una demostración)

Sabemos por el teorema de la suma y la resta que:

$cos(x pm y) = cos(x) cos(y) mp sin(x) sin(y)$

Si separamos la suma de la resta quedan entonces los dos posibles casos:

1): $cos(x + y) = cos(x)cos(y) - sin(x)sin(y)$
2): $cos(x - y) = cos(x)cos(y) + sin(x)sin(y)$

Si tomamos la ecuación 1) y despejamos cos(x)cos(y) nos queda que:

3): $cos(x)cos(y) = cos(x + y) + sin(x)sin(y)$

Y si sumamos el miembro de la derecha de la ecuación 2) al miembro izquierdo de la ecuación 3), y para mantener la igualdad se suma el lado izquierdo de la ecuación 2) en el lado derecho de la ecuación 3). (Recuerda que si se suma un elemento a ambos lados de la ecuación se mantiene la misma), quedaría:

cos(x)cos(y) + sin(x)sin(y) + cos(x)cos(y) = cos(x + y) + sin(x)sin(y) + cos(x - y)

Simplificando el elemento sin(x)sin(y) y sumando cos(x)cos(y) quedaría:

2cos(x)cos(y) = cos(x + y) + cos(x - y)

Y por ultimo multiplicando ambos lados de la ecuación por ½ queda:

$cos(x) cos(y) = {cos(x + y) + cos(x - y) over 2}$

Nota del autor: este procedimiento también se puede aplicar para demostrar el origen de las otras dos ecuaciones simplemente cambiando los valores...

Paso de Suma a Producto [editar]

Reemplazando x por (a + b) / 2 e y por (a – b) / 2 en las identidades de Producto a suma, se tiene:

$sin(a) + sin(b) = 2 sinleft( frac{a + b}{2} right) cosleft( frac{a - b}{2} right)$

$cos(a) + cos(b) = 2 cosleft( frac{a + b}{2} right) cosleft( frac{a - b}{2} right)$

$cos(a) - cos(b) = -2 sinleft( frac{a + b}{2} right) sinleft( frac{a - b}{2} right)$

$sin(a) - sin(b) = 2 cosleft( frac{a + b}{2} right) sinleft( frac{a - b}{2} right)$

Eliminar seno y coseno [editar]

A veces es necesario transformar funciones de seno y coseno para poderlas sumar libremente, en estos casos es posible eliminar senos y cosenos en tangentes.

$sin{left( x right)} = frac{tan{left( x right)}}{ sqrt{1 + tan^2{ left( x right)}} }$

$cos{left( x right)} = frac{1 - tan^2{left( frac{1}{2} x right)}}{1 + tan^2{left( frac{1}{2}xright)}}$

Funciones trigonométricas inversas [editar]

$arctan(x)+arctan(x)=left{begin{matrix} pi/2, & mbox{si }x > 0 \ -pi/2, & mbox{si }x < 0 end{matrix}right..$

$arctan(x)+arctan(y)=arctanleft(frac{x+y}{1-xy}right)$

Composición de funciones trigonométricas [editar]

$operatorname{sin}^2(arccos(x))=1-x^2$

$sin^2(arctan(x))=frac{x^2}{1+x^2}$

$tan[arcsin (x)]=frac{x}{sqrt{1 - x^2}}$

$tan[arccos (x)]=frac{sqrt{1 - x^2}}{x}$

$cos[arctan(x)]=frac{1}{sqrt{1+x^2}}$

$cos[arcsin(x)]=sqrt{1-x^2} ,$

$operatorname{cos}^2(arcsin(x))=1-x^2$

$cos^2(arctan(x))=frac{1}{1+x^2}$

Fórmula de productos infinitos [editar]

Seno	Coseno
$sin x = x prod_{n = 1}^inftyleft(1 - frac{x^2}{pi^2 n^2}right)$ $sinh x = x prod_{n = 1}^inftyleft(1 + frac{x^2}{pi^2 n^2}right)$ $frac{sin x}{x} = prod_{n = 1}^inftycosleft(frac{x}{2^n}right)$	$cos x = prod_{n = 1}^inftyleft(1 - frac{x^2}{pi^2(n - frac{1}{2})^2}right)$ $cosh x = prod_{n = 1}^inftyleft(1 + frac{x^2}{pi^2(n - frac{1}{2})^2}right)$

Fórmula de Euler [editar]

$e^{ix} = operatorname{cos{left( x right)}} + ioperatorname{ sen{left( x right)} }$

$e^{-ix} = operatorname{cos{left( x right)}} - ioperatorname{ sen{left( x right)} }$

Teorema del coseno [editar]

En todo triángulo «El cuadrado de un lado es igual a la suma de los cuadrados de los otros lados menos el doble del producto de estos lados por el coseno del ángulo comprendido...»

$a^2=b^2+c^2-2bccdotoperatorname{cos} A$

$b^2=a^2+c^2-2accdotoperatorname{cos} B$

$c^2=a^2+b^2-2abcdotoperatorname{cos} C$

Teorema del seno [editar]

En todo triángulo se da la siguiente relación entre la longitud de sus lados a, b y c y el seno de sus respectivos ángulos opuestos A, B y C

$frac{a}{sin(A)}= frac{b}{sin(B)} = frac{c}{sin(C)}$

Definiciones exponenciales [editar]

Función	Función inversa
$sin theta = frac{e^{itheta} - e^{-itheta}}{2i} ,$	$arcsin x = -i ln left(ix + sqrt{1 - x^2}right) ,$
$cos theta = frac{e^{itheta} + e^{-itheta}}{2} ,$	$arccos x = -i ln left(x + sqrt{x^2 - 1}right) ,$
$tan theta = frac{e^{itheta} - e^{-itheta}}{i(e^{itheta} + e^{-itheta})} ,$	$arctan x = frac{i ln left(frac{i + x}{i - x}right)}{2} ,$
$csc theta = frac{2i}{e^{itheta} - e^{-itheta}} ,$	$arccsc x = -i ln left(tfrac{i}{x} + sqrt{1 - tfrac{1}{x^2}}right) ,$
$sec theta = frac{2}{e^{itheta} + e^{-itheta}} ,$	$arcsec x = -i ln left(tfrac{1}{x} + sqrt{1 - tfrac{i}{x^2}}right) ,$
$cot theta = frac{i(e^{itheta} + e^{-itheta})}{e^{itheta} - e^{-itheta}} ,$	$arccot x = frac{i ln left(frac{i - x}{i + x}right)}{2} ,$
$operatorname{cis} , theta = e^{itheta} ,$	$operatorname{arccis} , x = frac{ln x}{i} ,$